A general theoretical approach to the study of advective effects on biological oceanographic dynamics is formulated and some simple examples are presented. The theory of characteristics provides a model which rigorously combines aspects of local biological dynamics with consideration of fluid particle flow along Lagrangian trajectories. A local kinematical analysis is carried out for gradients both of velocity and of biological state variables. This is followed by a study of the effects of a stretching deformation, which contains a frontogenetic effect, on one to three component biological systems. Problems include the approach to local biological equilibria and the stabilities of the equilibrium states; the competition between biological and advective equilibria; and nonlinear grazing processes and nutrient utilization.

Biological dynamics in the sea involves interactions among physical, biological and chemical processes and coupled processes. A multitude of scales and phenomena are involved, many of which are as yet unknown. Research in interdisciplinary theory and modeling is accelerating, and relevant studies range from idealized isolated process studies to attempts at simulating complex and realistic oceanic dynamics. Concomitantly biological dynamical studies are carried out in zero, one, two and three spatial dimensions. One aspect of the interpretation of some zero-dimensional studies involves the concept of local biological dynamics and equilibria. In such cases the physics may be assumed to be unimportant or may be parameterized by scale-separation hypotheses.

Physical processes which influence the biology consists of physiological effects such as temperature-dependent processes, diffusion and mixing, and advection. Physical processes may compete with or enhance biological processes. Advective effects, which are perhaps least well understood theoretically, are isolated as the focus of the present study. Advection involves the movement of biological material via the physical flow field. Vertical and horizontal velocities transport and entrap dissolved and particulate matter over multiple scales in space and time. A large variety of relevant phenomenological flow structures occur in the ocean, and their associated advective effects may be best treated deterministically or statistically.

The present study adopts an idealized general theoretical approach to the study of advective effects. The attempt is to identify and expose some basic processes which may aid in the interpretation of simulations and which may form the basis of further more realistic studies. The focus is primarily upon the influence of a deformation gradient in the flow field on a dynamically active tracer field, and the results may have some general applications to e.g. chemical and engineering dynamics. The general model, which can be related to zero-dimensional biological dynamics and fluid particle trajectories, is introduced in §2. Sections 3, 4 and 5 subsequently deal, respectively, with advective, biological and interactive processes. Section 6 summarizes and concludes.

(a) Formulation

Consider an n-component biological system with the state variables

The advective derivative in Cartesian coordinates is

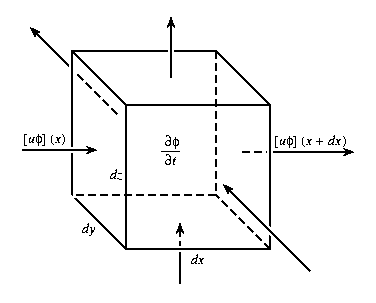
The advective derivative D/Dt, as given by equation (2.4a), represents the time rate of change of f_i following the fluid motion, but expressed in the Eulerian viewpoint for a space-time field (equation (2.1)) at a fixed point in the flow (Lamb, 1932, Chapter 1; Batchelor, 1967, Chapter 2). From the Lagrangian viewpoint, i.e., following tagged fluid particles along finite trajectories, zero-dimensional biological dynamics is simply occurring within each particle. Equation (2.4b) presents an alternative useful interpretation of the advective process at a fixed Eulerian point from a flux viewpoint. Taking into account all processes which act as effective sources (or sinks), equations (2.2) and (2.3) are simply point-wise statements of the conservation of f_i. The local advective flux (units of mass per unit area per unit time -ml^-2t^-1) is

Figure 1. At the fixed point (x,y,z) the net difference of rate of inflow and outflow of f through the six faces tends to change the amount of f within the infinitesimal volume.

In the present study we will restrict ourselves to two (spatial) dimensional flows, whence continuity implies the existence of a stream function y(x,y,t) such that

It will be convenient to express the model in both dimensional (2.10a) and nondimensional (2.10b) forms. For the latter case: the f_i will all be scaled by a representative mass density M; time by t₀; distance by L; and speed by u₀. Since the context will be clear, we will use identical symbols for both the dimensional and nondimensional versions for the dependent and independent variables. Thus the final model takes the forms

The left-hand side alone represents local time change plus the advection of the scalar field and the right-hand side alone, the ``zero-dimensional'' local biological dynamics. In general, scalar fields are characterized as passive or active depending upon whether or not they influence the flow field, and inert or dynamical depending upon whether they are simply advected or have sources and sinks due, e.g., to radioactivity, chemical reactions or biological activity.

A version of the parameter a (denoted S) based upon the growth rate t₀ = a_i0^-1 was first identified by Obrien and Wroblewski (1973) as an appropriate measure of advective effects. Platt and Denman (1975) and Platt et al. (1977) scaled a general biomass equation and estimated ranges of relative ratios from data available at that time, which are generally still relevant. A useful quantitative overview of the nondimensional approach is also presented by Wroblewski (1983). A recent example of a nondimensional analysis of scale-dependent physical and biological processes governing the distribution and variability of biomass for a particular species is provided by Horne and Schneider (1994).

(b) Solution

Equations (2.10) are a set of n-coupled first-order partial differential equations. Since the left-hand sides are linear in the f_i, and are identical operators on each of the f_i, it is a quasilinear set with the same principal parts which can be solved symbolically via the method of characteristics (Courant and Hilbert, 1989; Chapter II, Appendix I). Consider a solution given in terms of a parametric variable s in the form

The parametric initial value problem specifies data, without loss of generality, at s = 0. The initial values of all the variables are to be specified in terms of two additional parametric variables (r,q), since there are three independent variables in each of equations (2.10a,b). We designate

The structure of the formal solution of the preceding paragraph is dynamically interesting and provides a valuable framework for interpreting coupled biological and physical processes. Advective processes appear in (2.12a) directly in terms of the Lagrangian trajectory equations but in the s-domain. Similarly, the zero-dimensional biological dynamics appear in the s-domain in eq. (2.12b). A special but important class of problems involves the specification of initial fields in the time domain, i.e., at t = 0. The first of (2.12a) is always directly integrable to t = s+a(r,q), and for this special case we have a = 0, s = t. Now (2.12b) is the local biological dynamics, but the local ``biological equilibrium'' (2.15a) can be altered significantly by the advective effects through r,q as given by (2.14b).

To illustrate the solution procedure, we consider the simplest example of the exponential (Malthusian) growth of phytoplankton (f_i) with unlimited light and nutrient in the presence of a spatially uniform and constant velocity field (u₀,v_o). We seek the time evolution of an initial spatial distribution of f. Equations (2.12a,b) with reference to (2.10a) become

An alternative formulation of the model in terms of the stream function defined in equation (3.2) can be useful. We consider a time-independent stream function y(x,y) as an independent variable and seek f_i(y,y,t). Since

In this section we consider solutions to eqs. (2.10, 2.12) with B_i = 0 and (u,v) specified, i.e., the advection of a passive inert scalar. Even under these simplifications, analytical solutions for the trajectories are difficult and the flow of a tracer patch can be quite complex due to the stretching and folding of an initial distribution. Even smooth flows can give rise to chaotic advection (Ottino; 1989, 1990). Interesting examples of the complex trajectories that occur in oceanic mesoscale waves and coherent vortices are presented by Flierl (1981) and Dewar and Flierl (1985).

(a) Local analysis

Consider the initial value problem in the time domain. To provide some general insight we expand both an initial scalar tracer field and the advecting velocity in Taylor series in the neighborhood of the point (0,0). Since the tracer fields are inert and uncoupled we drop the subscript i. Thus

Insight into basic advective processes can be gained by a decomposition of the velocity gradient into its fundamental kinematic parts: divergence (x), stretching deformation (n), vorticity (w), shearing deformation (m)

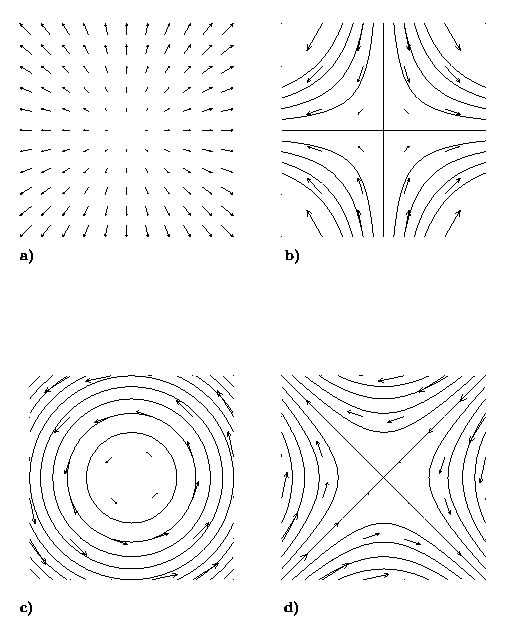
Figure 2. Fundamental kinematic components of a velocity gradient: (a) divergence; (b) stretching deformation; (c) vorticity; (d) shearing deformation.

To illustrate the effects of vorticity we set u₁ = 0 and u₂ = -v₁, whence w = 2v₁. Then g is imaginary and

To illustrate the effects of deformation we set v₁ = u₂ = 0; and the solution is now

(b) Frontogenesis

The role of deformation fields as a ``trigger'' mechanism for the generation of physical fronts in the atmosphere, or the signal that frontogenesis is occurring has been known for some time (Bergeron, 1928; Petterson, 1935). The analogous mechanisms is known to act as a causal mechanism for frontogenesis in the oceans (Simpson and James, 1986). Oceanic fronts have been identified as locations of intensified biological activity because of frontal upwelling of nutrients. It should also be recognized that the processes that cause strong physical gradients of e.g. temperature, will also tend directly to concentrate and cause strong gradients of biological and chemical tracers, i.e., to generate biological fronts. Convergence (regions of negative x) is also a frontogenetic kinematic mechanism, but the thin aspect ratios of the atmosphere and ocean (depth much less than horizontal scales) render them almost horizontally nondivergent and the process is less important.

Saucier (1953) describes a classical meteorological method for analyzing the tendency for frontogenesis from the horizontal deformation of wind fields. The angle (q) required for rotation of the axes into principal axes, and the resultant principal stretching deformation (n_p) are given by

(c) Oceanic gradients

Relatively intense gradients occur in the deep and coastal oceans associated with a variety of scales of motion, phenomena, and internal and external driving mechanisms. Permanent fronts separate water masses and give rise to intense boundary and free jets. Permanent convergence zones exist in the equatorial, subtropical and polar oceans. Water mass driven, wind-driven, and tidally driven fronts occur at and across shelf breaks, in the coastal ocean and in the vicinity of banks. Internal dynamical processes (e.g., instabilities, nonlinear and topographic interactions) populate the ocean with frontal ring vortices, eddies, and lenses over a range of meso- and submeso-scales. Such fronts and eddies must be expected to produce biological fronts and interactions and to influence biological dynamics. Biological and physical interactions for some types of fronts, have been and are being studied, such as: eastern boundary upwelling systems (Barber and Smith, 1981), cold and warm core Gulf Stream rings (The Ring Group, 1981; Olson and Backus, 1985; Franks et al., 1986); tidal fronts (Lynch et al., 1995); and eddy-eddy interactions (McGillicuddy et al., 1995). Others have only recently been discovered or understood and await interdisciplinary research.

A theoretical study (Kirwan et al., 1994) of aspects of nonlinear ocean dynamics is based in part on the local kinematics of horizontal divergence (x), deformation (n) and vorticity (w). Waves eddies and submesoscale lens are considered under various dynamical assumptions. Further and broader studies based in the kinematic approach can be useful to the theory of advective effects in biological dynamics. A number of relevant field studies have been carried out attempting to measure directly the kinematic quantities from the dispersion of float clusters. Inference of x, n and w is quantitatively difficult and usually sensitive (Kirwan et al., 1988, 1992). A recent study (Sanderson, 1995) was carried out on the Western Bank of the Scotian Shelf in which the drifters were part of a measurement and modeling system to track cod larvae (Bowen et al., 1995). The estimates, considered sensitive, were

w = (-1.9±0.06)×10^-5 s^-1, x = (-9.5±7)×10^-7 s^-1,

n = (9.0±7)×10^-7 s^-1, m = (1.7±0.6)×10^-6 s^-1.

Recall that (1.16)×10^-5s^-1 = (day)^-1. Thus such physical time scales are in the range of some important biological time scales (Denman and Powell (1984); Dickey (1990)). Some general scale considerations for effective biological and physical interactions are discussed by Steele (1988), Nihoul and Djendi (1991) and Denman (1992).

In this section we summarize some of the dynamical properties of a simple two-component biological system in zero spatial dimensions (e.g., Freedman (1980); Murray (1993)). We assume a predator-prey system with perfect grazing. In the absence of grazing, the prey can achieve an equilibrium value (carrying capacity) but the predator is depleted, e.g., a simple phytoplankton-zooplankton model with unlimited light and nutrient to support photosynthesis.

The relevant equations are (2.2) and (2.6) with nondimensionalization when desirable as in (2.10) but with u₀ = 0. To keep all of the constants in the equations positive, we adopt the notation [^a]_ij = -a_ij if a_ij < 0, and similarly for a_ij. The model equations under the above assumptions are, with a₁₂ = -a₂₁ and a₂₂ = 0,

Let F_i denote a steady state equilibrium field and introduce the notation

(a) The null state

For instability analyses we assume d,e to be infinitesimal. Then linearization of (4.1a,b) about the null state (4.4a) decouples the two fields and f₁ is unstable and f₂ is stable. If the f₂ perturbation is suppressed, f₁ will evolve in time to the carrying capacity equilibrium C. If e ¹ 0, f₂ will begin to grow when the second term on the rhs of (4.1b) exceeds the first term. Nondimensionalizing both state variables by M = C and choosing t₀ = (a₁₀)^-1, eqs. (4.1) become (vid. (2.10c))

(b) Carrying capacity

The carrying capacity equilibrium is governed by equations (4.5) with f₂ º 0 and d = f₁-1. The full d equation is

To study grazing we nondimensionalize the time by t₀ = (a₂₁M)^-1, with M as an arbitrary biomass density. Equations (4.1) become

Next we present the solution for the nonlinear conversion of prey to predator for the limiting case that the grazing rate is much faster than growth and mortality rates. From equation (4.8) this limit is seen to require

The effect of mortality of the predator can be treated analytically via singular perturbation theory when the mortality rate is small but finite. Thus we keep a₁₀ = [^(a)]₁₁ = 0 but retain [^(a)]₂₀ << 1 in (4.8) as the perturbation parameter. The solution (4.10b) for the prey is unaltered but the solution for the predator is now

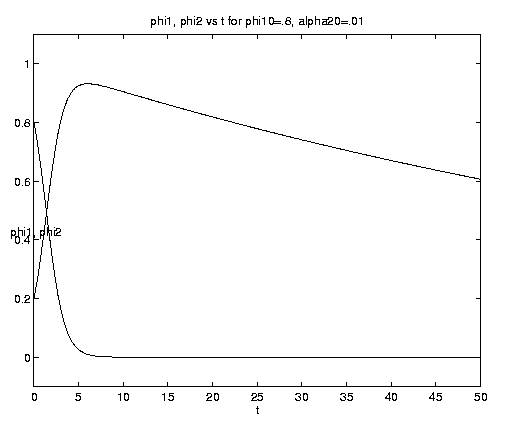
Consider for example f₁ as a chemical nutrient and f₂ as phytoplankton. After consuming almost all the nutrient in the dimensional time scale (a₂₁M)^-1 the phytoplankton slowly die off on the dimensional time scale (a₂₁G)^-1, as shown on figure 3(c). The plankton f₂ asymptotically approach zero identically but there is a small residual amount of nutrient f_1¥ which can be computed from the exact integral of the system. Equation (4.10d) is now replaced by

(d) N-P-Z Model

The nonlinear conversion results are extended to a three component system. The phytoplankton f₁ = P are grazed by the zooplankton f₂ = Z while they consume the nutrient f₃ = N. We assume perfect grazing (a_ij = -a_ji) and neglect mortalities (a_io = a_ii = 0). The non dimensional model equations, with all biomasses scaled by M and t₀ = (a₁₃M)^-1, are

The parameter b = a₂₁ (a₁₃)^-1, the ratio of the grazing interaction coefficients, measures the relative rate of zooplankton depletion of phytoplankton to their growth rate via nutrient consumption. Addition of the three equations and an integration after eliminating P from (4.11b,c), yields two integrals of the system

To facilitate the study of advective effects we seek relatively simple solutions to the zero-dimensional biological dynamics. Thus we will take the exact solution for b = 1 and approximate solutions for general b. For b = 1, (4.12c) integrates to

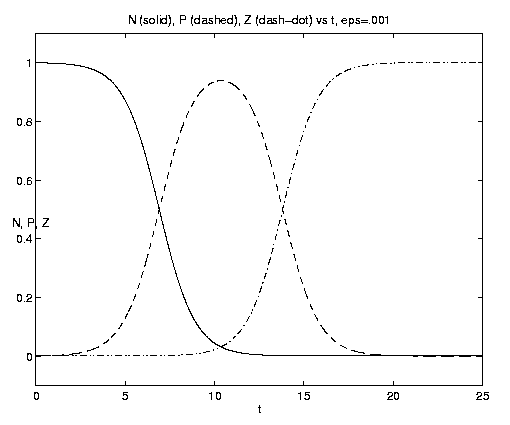
If b = 0, the system reduces to the two components (N,P) and the solution becomes

From (4.11a) we note that the initial rate of plankton growth is given by P₀ (N₀ - bZ₀). Thus if b << 1, N₀ will first be converted to P via the 2-component process described by equation (4.12i), followed by a similar two-component conversion of N₀ to Z but on the longer time scale b^-1. For b > N₀ Z₀^-1, P decreases immediately at t = 0 and cannot efficiently act as a conduit for the growth of Z. For b >> N₀ Z₀^-1 Z can only convert P₀, and asymptotically N_¥ = N₀, P_¥ = 0, Z_¥ = Z₀ + P₀. Thus rapid grazing is disadvantageous for the zooplankton.

An interesting case lies in the determination of asymptotic values in the range N₀ Z₀^-1 > b > 1; for conditions (4.12f) this becomes b < O(e^-1). There is an initial growth of plankton to a maximum value P_m with associated values Z_m, N_m, at t = t_m. From (4.11a) N_m = bZ_m when P_t = 0. From (4.12a,b,f)

e	b	Zm	Nm	Pm	Z¥	N¥
0.0010	5.0000	0.0827	0.4135	0.5058	0.7508	0.2512
0.0010	10.0000	0.0658	0.6579	0.2783	0.5008	0.5012
0.0010	15.0000	0.0513	0.7691	0.1816	0.3710	0.6310
0.0010	100.0000	0.0098	0.9775	0.0148	0.0687	0.9333
0.0100	5.0000	0.1214	0.6070	0.2916	0.6219	0.3981
0.0100	10.0000	0.0811	0.8111	0.1278	0.3890	0.6310
0.0100	15.0000	0.0592	0.8882	0.0726	0.2844	0.7356

In this section we consider the occurrence of the biological processes of the previous section in the presence of a dynamically interesting flow field with deformation. We will present results for the competition between physical and biological effects for: the stability analyses, the nonlinear approach to carrying capacity or advective equilibria, and nonlinear grazing.

The parameter a = u₀t₀L^-1 (equation (2.10c)) measures the relative importance of advective to biological effects if t₀ is chosen as the characteristic time of the dominant biological process. As for equations (3.4) we choose v₁ = u₂ = 0 in (3.2) and set u₀L^-1 = u₁, the deformation gradient of the flow field y = -u₁xy. Equations (2.10), (2.11), (2.12) in nondimensional form appear as

(a) Linearized instabilities of equilibria

Since a > 0 always, q = ye^at represents exponential growth, and the presence of an initial spatial gradient of f_i can significantly alter stability properties in the presence of the physical flow. Stable solutions can be rendered unstable and instabilities will occur with enhanced growth rates.

Linearity allows separability, thus

For the null state (4.6) the instability of the prey is enhanced and the stability of the predator can be switched to instability if the advective supply rate exceeds the decay rate. Sufficient advection can also destabilize both the carrying capacity (4.7) and grazing states (4.9); the Lotka-Volterra model in the presence of deformation advection is always switched from neutral stability to instability. The quantitative conditions among the biological rate and interaction parameters and the deformation shear are given in Table 2.

State	a	Condition	Effect
null	u1a10	a > [^(a)]20 or  u1 > a20(a10)-2	predator
			unstable
carrying	u1a10	a > 1             u1 > (a10)-1	instability
capacity
grazing	u1[^a]20	2a > [^(a)]11            u1 > [^a]11(a21[^a]20)-1	instability

Okubo (1980, Chapter 10) reports a stabilization of the Lotka-Volterra model when the predator and prey tend to migrate towards a central favorable region with constant velocities in the presence also of diffusion.

(b) Carrying capacity vs. advective equilibria

Here we consider the behavior of the one component biological system, e.g., phytoplankton (4.7), in the presence of the deformation advection of equation (5.1). The solutions are now given by (4.7c,d) with d₀, f₁₀ replaced by functions of q as in (5.1c).

First we generalize the stability analysis of equation (5.2) for case g₀ = 0, g₂ = 1. Now M = C and L = Cc₂^-1. The nonlinear solution for the departure from equilibrium is

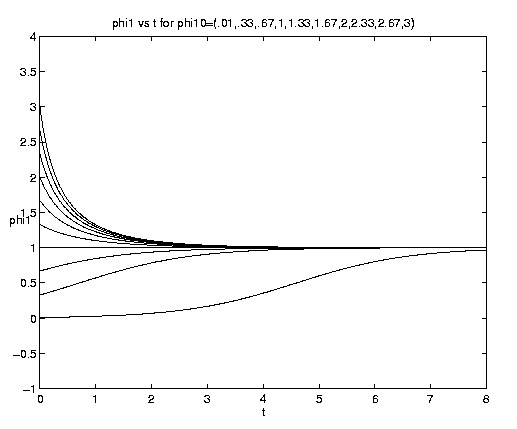
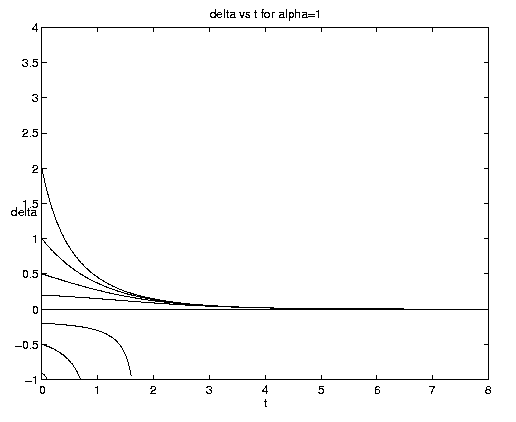
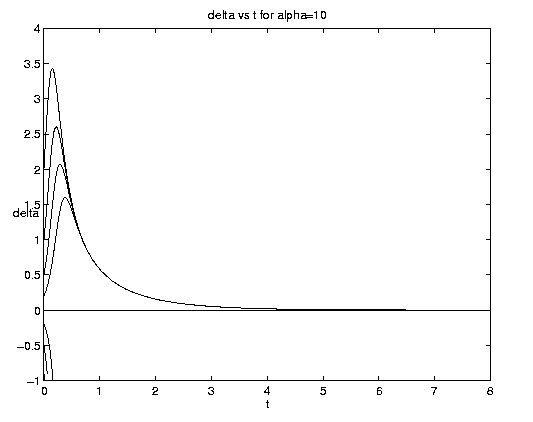
The limit of pure advection is given by d = d directly by (5.3c) or equivalently by setting e^t = 1 in (5.3a) but retaining e^at. The limit of pure biology is given by a = 0. Both of these limits are plotted on figure 4(a). Advection is plotted for a = 1, i.e., with equal advective and biological time scales. To interpret these and subsequent plots note that at t = 0, d = y, so that a curve emanating from a point d^* on the ordinate axis represents d(y = d^*,t). The biological behavior is of course identical to that shown on figure 3(a). The advective solutions for y > 0 amplify indefinitely but for y < 0 reach the limiting value d = -1 at time t_-1 = ln(-y^-1) and remain at that value thereafter. This behavior is consistent with the deformation flow (vid. figure 2(b)) ultimately advecting in fluid with no phytoplankton for y < 0 but advecting in fluid with an ever increasingly dense population for y > 0.

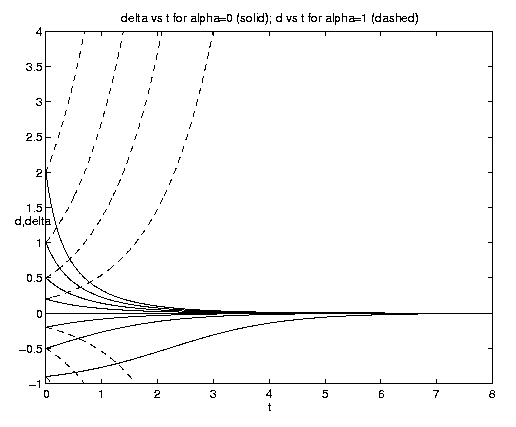
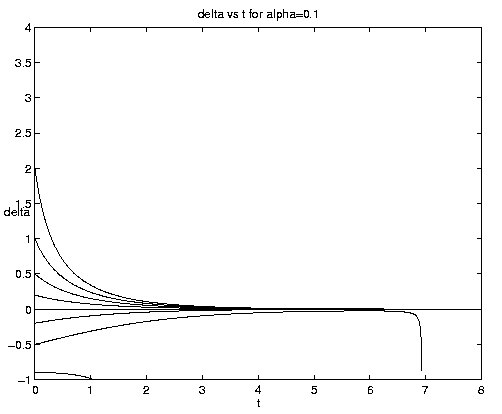
Figure 4. Carrying capacity vs. advective equilibria: (a (above) ) Pure advection (dashed) and pure biology (solid); (b (below) ) dependance on relative strength of advection [Click on components of 4b for increased resolution].

The general interactive solution is illustrated on figure 4(b) for values of a = (0.1,1,10) which range from relatively weak to strong advective effects and span all qualitative behaviors. The solutions equation (5.3a) have maxima at t = t_m for both positive and negative y but only for a range of values. The times at which maxima and limiting values are reached are

Asymptotically in time an excess initial population always approaches the carrying capacity equilibrium but a deficit population approaches the advective null equilibrium.

Examination of figure 4(b) shows some interesting effects. Frontogenesis occurs, ultimately producing a very sharp front of unit strength. For large a and positive y, advection dominates until the maximum is reached at t_m and a much stronger but broader front is present. For large a and negative y advection dominates with but little biological modification before t_-1. For small a advection has little effect on the approach to the biological equilibrium for positive y. For negative y and small a, however, the solutions are dominated by almost pure biological behavior for a long time, i.e., until t_m >> 1. Biological equilibrium is very nearly achieved whence advection suddenly sweeps away the population. This is because (equations (5.3)) for a << 1, t_m » t_-1. The curve emanating at y = -.20 for a = 0.10 which is indistinguishable from zero at t = 8 has the associated values t_m = 15.04, t₁ = 16.09.

The next problem deals with the identical dynamics as the previous one but for the initial condition introduces a finite frontal width L across which the biomass density changes from zero to a maximum value of F. We retain the biomass scaling M = C as introduced prior to equation (5.3a). The initial condition is now taken as

The approach to equilibrium is now given by

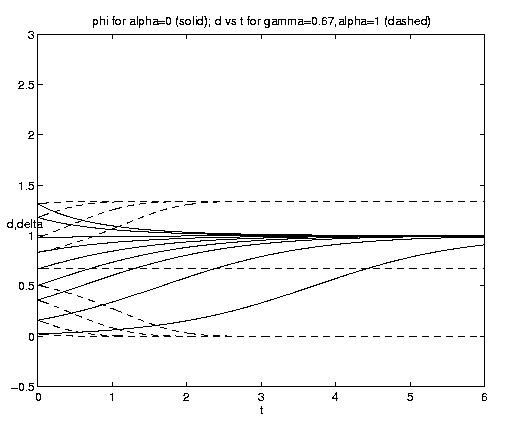
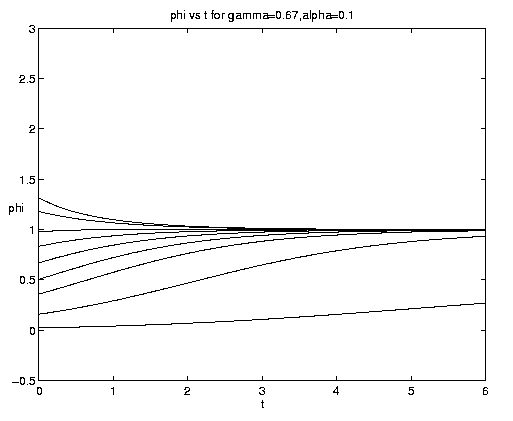
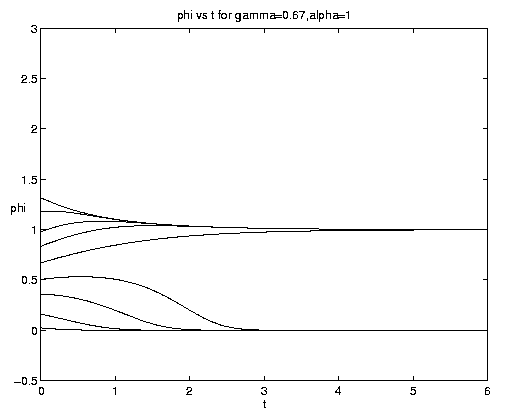
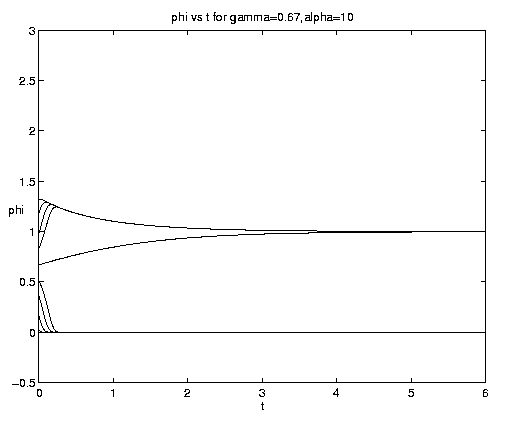
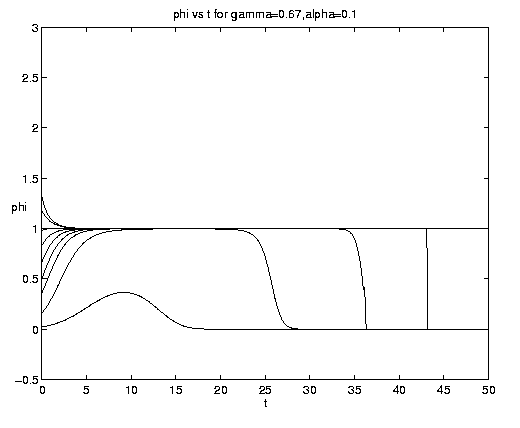
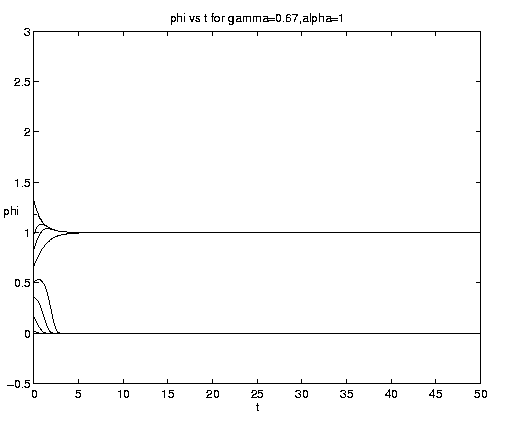
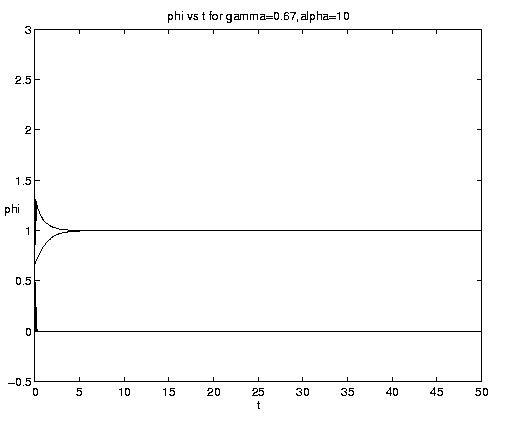
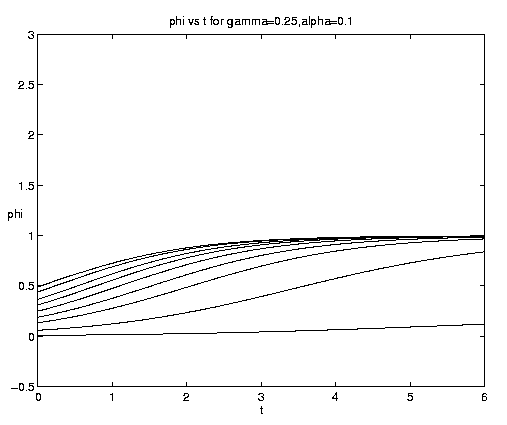
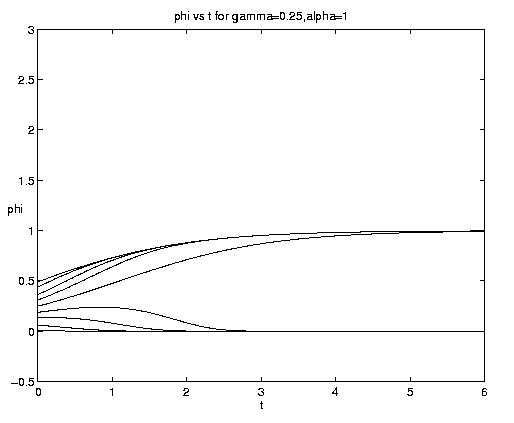
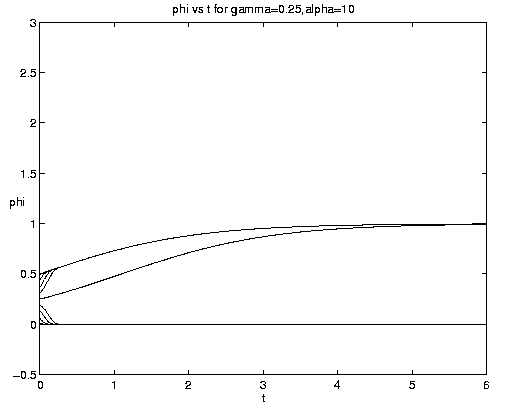
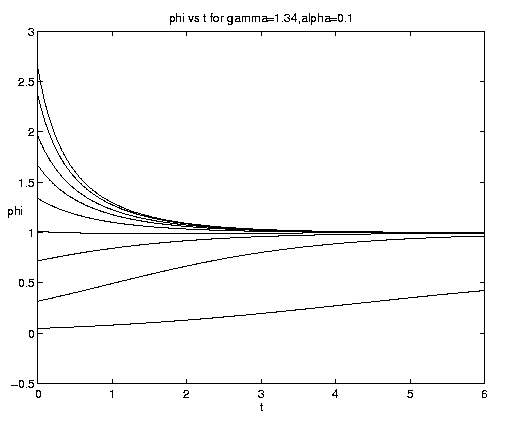
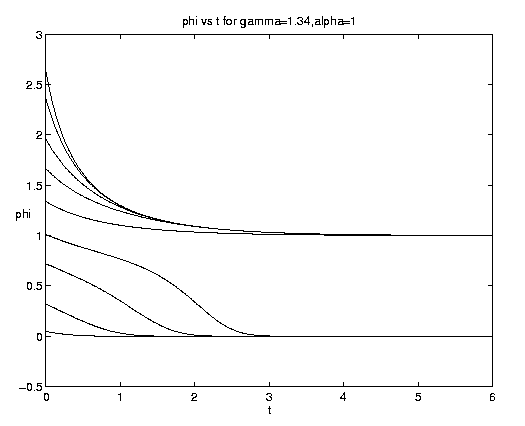
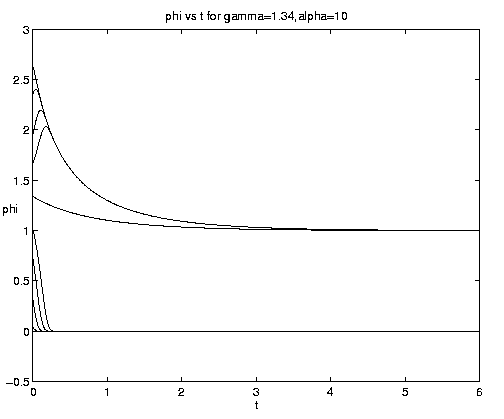
The range of qualitative behavior of solution (5.4) as a function of the relative rate and frontal strength parameters (a,g) is illustrated on figure 5. Figure 5(a) presents the pure biological and pure advective limits. Figures 5(b,c) are for an initial frontal strength (2g) somewhat larger than the carrying capacity and Figures 5(d,e) show the behavior for a weaker (stronger) front. Figure 5(c) illustrates a small a behavior analogous to that on figure 4(b).

Figure 5. As for Fig. 4 but for a finite front: (a) Pure advection (dashed) and pure biology (solid); (b) and (c) initial frontal strength somewhat larger than carrying capacity and show, respectively, the short and long time behavior; (d) initial frontal strength smaller than carrying capacity; (e) initial frontal strength much larger than carrying capacity.

(c)Grazing with advection

The effects of advection on grazing are particularly interesting since advective supply of nutrients can dominate the qualitative and quantitative behavior of the biological dynamics. We retain the deformation flow field of equation (5.1). For definiteness of interpretation, we can consider solutions in the half-plane y > 0 as representing an infinitely deep ocean with sea surface at y = 0. Thus advection can be regarded as bringing material from the deep sea into the surface region. The models remain of course highly ideaized and we do not intend to imply any direct realistic oceanic relevance.

The advective process introduces a new advective equilibrium state. Introducing the biology of equations (4.10) into equations (5.1a,b) and setting [(¶)/(¶t)] = [(¶)/(¶x)] = 0 yields

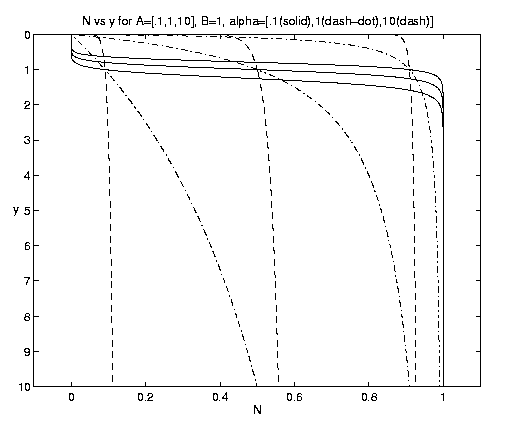
Figure 6. Advective equilibrium profiles [alpha = .1 (solid), 1 (dash-dot), 10 (dashed)]. The A dependence is indicated by where the alpha triplets intersect at y = 1. For A = (.1,1,10), the intersections at y = 1 are at N = (.9,.5,.09), respectively.

We need consider only equations (4.11)-(4.13) since they contain the dynamics of (4.10) for the case of b = 0. For all solutions we will take the initial plankton fields as a small uniform background constant. The initial nutrient field will be a linear increase of N with depth y, and interest will be restricted to order unity depths. Thus

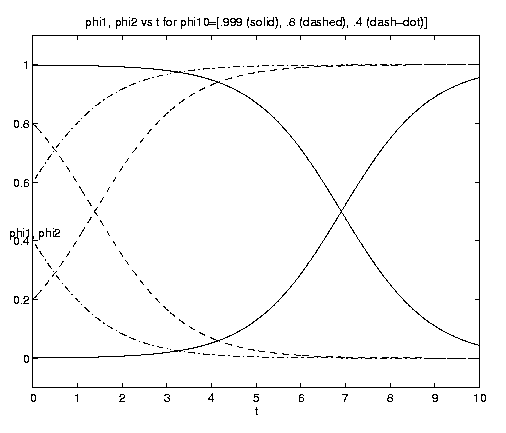
For the two-component NP system figure 7 illustrates the dependence of the grazing on the initial condition (e) and the advective parameter (a). Figure 7(a) shows an initial advective growth of P followed by a complete depletion via grazing. It is important to note that after some times the solution is independent of the value of the initial phytoplankton biomass, which simply controls the amplitude and time of occurrence of the maximum of N. Figures 7(b,c) for fixed e = .001 illustrates the dependence on the advection rate. Rapid advection results in an early, large amplitude maximum in N and an early rapid growth of P asymptotically.

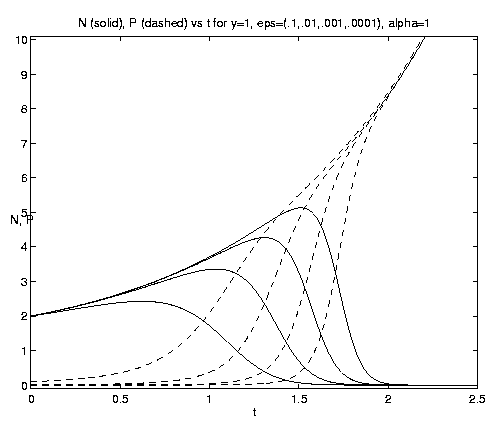
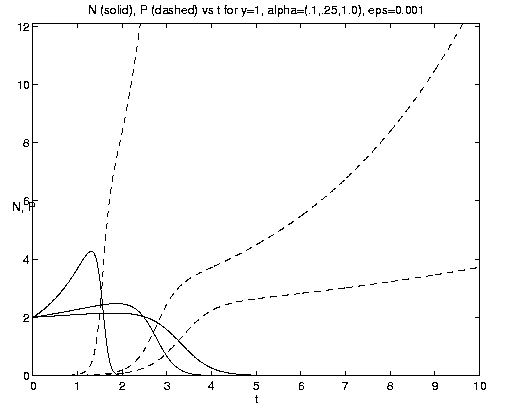
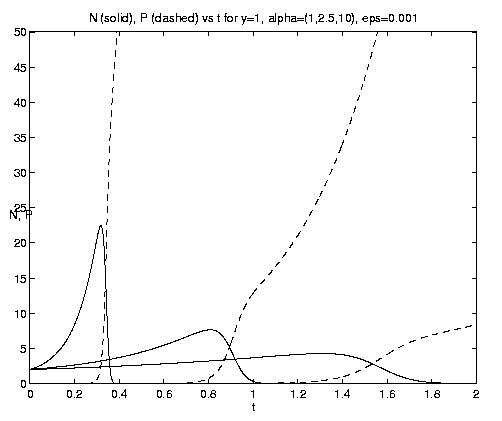
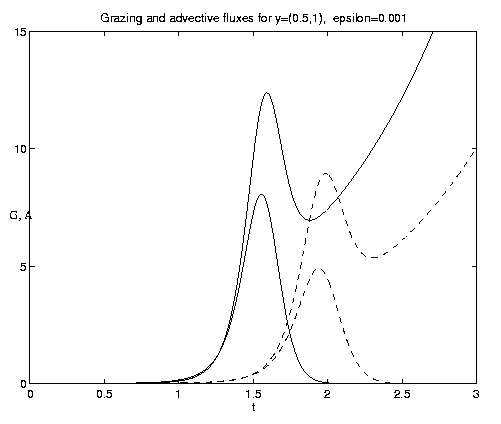
Figure 7. NP conversion: (a) Dependence on initial conditions; (b) weak and moderate advection [N = solid, P = dashed]; (c) moderate and strong advection [alpha = 1.0 (solid), 2.5 (dash-dot), 10 (dashed)], as a increases, the maximum in N increases and the conversion to P occurs earlier; (d) grazing and advection rates [y = 0.5 (dashed), 1.0 (solid)], as time increases local grazing stops.

Recall that if there were no planktons (Z = P º 0) the purely advective solution for the inert passive nutrient would be given by (5.6b) (vid equation (3.4b)). In the advective NP system (b = 0) for large t

The behavior of the three-component NPZ system for equal grazing rates (b = 1) is shown on figures 8(a,b) for the same values of e and a and the same scales as figures 7(b,c) for comparison. As indicated by equation (4.12h), the advected nutrient is now asymptotically completely converted to Z with ultimately no observable N or P. The rate of the processes again increases with increasing a, as do the amplitudes of the successive maximum values of N and P. For b >> 1, 1 ³ eb, the fraction of nutrient effectively utilized by P and Z and its partioning between them, is given by (4.13c). N and Z will now both be observed to grow exponentially after the initial adjustment time. In this model, rapid grazing by zooplankton leads to a smaller Z biomass than slow grazing.

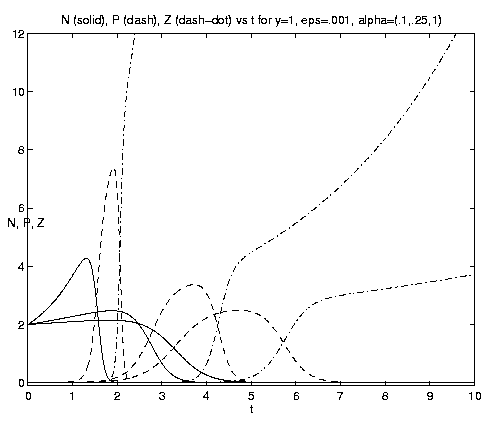
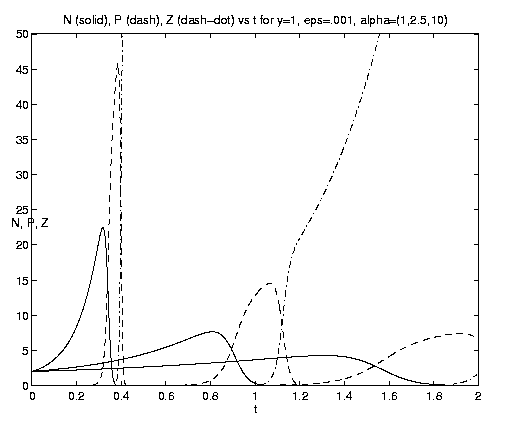
Figure 8. NPZ conversions: (a) Weak and moderate advection [N = solid, P = dashed, Z = dash-dot]; (b) moderate and strong advection, maxima in N and P increase with increasing a and the rapid growth of Z occurs earlier.

This study presents a general theoretical structure for the analysis of advective effects on biological dynamics in the sea. It is based upon the mathematical theory of characteristics and, in the domain of the parameter s, involves the zero-dimensional local biological dynamics, as well as the Lagrangian trajectories of the fluid particles. The s-domain initial value problems solved here were for the case that s was identified with the time t, and involved the specification of space-wise initial fields at t = 0. More general problems are possible and should be considered.

A kinematical analysis of the flow field was introduced and the effects of divergence, vorticity, stretching and shearing deformations on local gradients of biological state variables were discussed. The stretching deformation flow, which contains frontogenesis and frontolysis effects that contract and dilate gradients, was selected for the present study. The biological dynamical system included net birth or mortality, self-interactions and coupled field interactions. Biological processes subjected to advection included: the approach to local equilibria; the stability or instability of equilibrium states for one, two, or three-component systems; and nonlinear grazing conversions for NP and NPZ models. Further research should be directed towards additional and more realistic flow structures (vorticity, divergence, three dimensions, time-dependence, and nonlocal circulation structures, etc.) as well as additional and more realistic biology (Michaelis-Menten grazing, light limitation, behavior, etc.).

Advection by a deformation shear field in the presence of local gradients of the biological state variables was found capable of destabilizing null, carry-capacity and grazing equilibria and the velocity shear required was obtained in terms of the biological growth (death) rates and interaction coefficients. The competition between local biological and advective equilibria in the presence of frontogenesis was illustrated both for a simple deformation field flow and for a front of finite width. For an NPZ model the concept of advective-grazing equilibria was introduced and exemplified. For the cases of initial small background distribution of planktons in the presence of a deep ocean reservoir of nutrient the growth and conversion of planktons were calculated including the asymptotic in time partitioning of the advective nutrient input among the NPZ variables. At large times, P does not survive and Z is most successful by slow rather than rapid grazing.

These first results indicate the utility of the approach and provide some insight for further research. Deformation fields occur over a range of scales in the ocean and in other fluids in which dynamic tracers are of interest for a variety of reaction and nonconservative dynamics. Biological rates and physical advection times of interest in the ocean range from hours to days to weeks to months and seasons. A comprehensive review of time scales in the context of this theory could serve both to constrain the theory and guide developments. In addition to the direct extensions discussed in the preceding paragraphs it would be of interest to carry out first studies including new processes such as chaotic trajectories, mixing, swimming and small-scale encounter dynamics. The formulation of more general initial value problems in the s-domain should be guided not only by direct biological considerations but also by the mathematical structure of the theory of characteristics.

This research was stimulated by several interesting, important and enjoyable scientific discussions with Prof. Brian J. Rothschild. I thank Profs. A. Denny Kirwan, Jr. and Eileen E. Hofmann and Drs. Patrick J. Haley, Jr. and Dennis J. McGillicuddy for helpful scientific and mathematical comments. I am grateful to Mr. Wayne G. Leslie for his essential contribution to this study by the performance of sensitivity analyses and the preparation of figures. It is a pleasure to thank Dr. Nadia Pinardi for the hospitality of Istituto per lo studio delle Metodologie Geofisiche Ambientali (CNR-IMGA) during a sabbatical visit. The preparation of the manuscript by Ms. Marsha A. Glass and Mrs. Renate D'Arcangelo is very much appreciated. This research was supported in part by the Office of Naval Research under grant N00014-95-1-0371 to Harvard University.

Barber, R.T. & Smith, R.L. 1981 Coastal and estuarine fronts. In Analysis of Marine Ecosystems (ed. A.R. Longhurt). New York: Academic Press.

Batchelor, G.K. 1967 An introduction to fluid dynamics. Cambridge: Cambridge University Press.

Bergeron, T. 1928 Über die dreidimensionale verknüpfende Wetteranalyse I. Geofis. Pub. 5(6), 1-111.

Bowen, A.J., Griffin, D.A., Hazen, D.G., Matheson, S.A. & Thompson, K.R. 1995 Ship-board nowcasting of shelf circulation. Cont. Shelf Res. 15, 115-128.

Courant, R. & Hilbert, D. 1989 Methods of mathematical physics. In Partial Differential Equations, vol. II, 830pp. New York: Wiley Interscience.

Denam, K.L. & Powell, T.M. 1984 Effects of physical processes on planktonic ecosystems in the coastal ocean. Oceanogr. Mar. Biol. Annu. Rev. 22, 125-168.

Denman, K. 1992 Scale determining biological/physical interactions in oceanic food webs. In Aquatic Ecology; Scale, Pattern and Process (ed. P.S. Giller, A.G. Hildrew & D.G. Raffaelli). Oxford: Blackwell.

Dewar, W.K. & Flierl, G.R. 1985 Particle trajectories and simple models of transport in coherent vortices. Dyn. Atmos. Oceans 9, 215-252.

Dickey, T.D. 1990 Physical-optical-biological scales relevant to recruitment in large marine ecosystems. In Large Marine Ecosystems: Patterns, Processes, and Yields (ed. K. Sherman, L.M. Alexander & B.D. Gold), Publ. no. 90-30s, pp. 82-98. Washington, DC: Am. Assoc. Advanc. Sci.

Flierl, G.R. 1981 Particle motions in large amplitude wave fields. Geophys. Astrophys. Fluid Dyn. 18, 39-74.

Franks, P.J.S., Wroblewski, J.S. & and Flierl, G.R. 1986 Prediction of phytoplankton growth in response to the frictional decay of a warm-core ring. J. Geophys. Res. 91(C6), 7603-7610.

Freedman, H.I. 1980 Deterministic models in population ecology, 254pp. New York and Basel: Marcel Dekker, Inc.

Hinze, J.O. 1975 Turbulence. New York: McGraw-Hill, 790pp.

Horne, J.K. & D.C. Schneider 1994 Analysis of scale-dependent processes with dimensionless ratios. OIKOS 70, 201-211.

Hoskins, B.J. 1982 The mathematical theory of frontogenesis. Annu. Rev. Fluid Mech. 14, 131-151.

Kirwan, A.D., Jr. 1988 Notes on the cluster method for interpretating relative motions. J. Geophys. Res. 93(C8), 9337-9339.

Kirwan, A.D., Jr., Lewis, J.K., Indest, A.W., Reinersman, P. & Quintero, I. 1988. Observed and simulated properties of loop current rings. J. Geophys. Res. 93(C2), 1189-1198.

Kirwan, A.D., Jr., Indest, A.W., Liu, J. & Clark, N. 1990 Ring evolution in general circulation models from path analysis, J. Geophys. Res. 95(C10), 18,057-18,073.

Kirwan, A.D., Jr., Lipphardt, Jr., B.L. & and Liu, J. 1992 Negative potential vorticity lenses. Int. J. Eng. Sci. 30(10), 1361-1378.

Kirwan, A.D., Jr., Lipphardt, B.L., Jr. & Gregory, K.L. 1994 Nonlinear ocean dynamics. In The Oceans: Physical-Chemical Dynamics and Human Impact (ed. S.K. Majumdar, E.W. Miller, G.S. Forbes, R.F. Schmalz & A.A. Panah). Easton, PA: The Pennsylvania Academy of Science, pp. 40-55.

Klein, P. & Steele, J.H. 1985 Some physical factors affecting ecosystems. J. Mar. Res. 43, 337-350.

Lamb, H. 1932 Hydrodynamics. Cambridge: Cambridge University Press.

Lynch, D.R., Ip, J.T.C., Naimie, C.E. & Werner, F.E. 1995 Convergence studies of tidally-rectified circulation on Georges Bank. In Quantitative Skill Assessment for Coastal Ocean Models (ed. D.R. Lynch & A.M. Davies), Coastal and Estuarine Studies, Am. Geophys. Union 47, pp. 153-174.

McGillicuddy, D.J., Robinson, A.R. & McCarthy, J.J. 1995 Coupled physical and biological modelling of the spring bloom in the North Atlantic (II): Three-dimensional bloom and post-bloom processes. Deep Sea Res. I 42(8), 1359-1398.

Murray, J.D. 1993 Mathematical biology. Berlin: Springer-Verlag, 767pp.

Nihoul, J.C.J. & Djenidi, S. 1991 Hierarchy and scales in marine ecohydrodynamics. Earth-Sci. Rev. 31, 255-277.

O'Brien, J.J. & Wroblewski, J.S. 1973 On advection in phytoplankton models. J. Theor. Biol. 38, 197-202.

Okubo, A. 1980 Diffusion and ecological problems: Mathematical models, 254pp. New York: Springer-Verlag.

Olson, D.B. & Backus, R.H. 1995 The concentrating of organisms at fronts: a cold-water fish and a warm-core Gulf Stream ring. J. Mar. Res. 43, 113-137.

Ottino, J.M. 1989 The kinematics of mixing: Stretching, chaos, and transport. Cambridge: Cambridge Univ. Press.

Ottino, J.M. 1990 Mixing, chaotic advection, and turbulence. Annu. Rev. Fluid Mech. 22, 207-253.

Petterson, S. 1935 Contribution to the theory of frontogenesis. Geofis. Pub. 11(6).

Platt, T., Denman, K.L. & Jascy, A.D. 1977 Modeling the productivity of phytoplankton. In Marine Modeling, The Sea (ed. E.D. Goldberg, I.N. McCave, J.J. O'Brien, & J.H. Steele), vol. 6, pp. 807-856. New York: J. Wiley & Sons.

Platt, T. & Denman, K.L. 1975 A general equation for the mesoscale distribution of phytoplankton in the sea. Mem. Soc. of Sci. Liege 7, 31-42.

Pond, S. & Pickard, G.L. 1978 Introductory Dynamical Oceanography. Oxford, England: Pergamon Press, 241pp.

Ring Group, The 1981 Gulf Stream cold-core rings: their physics, chemistry, and biology. Science 212, 1091-1100.

Sanderson, B.G. 1995 Structure of an eddy measured with drifters. J. Geophys. Res. 100(C4), 6761-6776.

Saucier, W.J. 1953 Horizontal deformation in atmospheric motion. Transact. Am. Geophys. Union 34(5), 709-719.

Simpson, J.H. & James, I.D. 1986 Coastal and estuarine fronts. In Baroclinic Processes on Continental Shelves (ed. C.N.K. Mooers). Washington, DC: Am. Geophys. Union, pp. 63-93.

Steele, J.H. 1988 Scale selection for biodynamic theories. In Toward a Theory on Biological Physical Interactions in the World Ocean (ed. B.J. Rothschild). Dordrecht, The Netherlands: Kluwer Academic Publishers, pp. 513-526.

Stewart, H.J. 1945 Kinematics and dynamics of fluid flow. In Handbook of Meteorology (ed. F.A. Berry, Jr., E. Bollay, & N.R. Beers), pp. 412-419. New York: McGraw-Hill.

Stone, P.H. 1966 Frontogenesis by horizontal wind deformation fields. J. Atmos. Sci. 23(5), 455-465.

Williams, R.T. 1967 Atmospheric frontogenesis: A numerical experiment. J. Atmos. Sci. 24, 627-641.

Wroblewski, J.S. 1983 The role of modeling in biological oceanography. Ocean Sci. and Eng. 8(3), 245-285.